Uno de los objetivos de la educación es desarrollar en los niños y jóvenes las competencias necesarias para solucionar eficazmente las situaciones que les plantea el entorno, con apoyo de su pensamiento matemático, ya que la solución de problemas es uno de los cinco procedimientos generales que involucra dicho pensamiento, además de la modelación de fenómenos de la realidad, de la comunicación, del razonamiento y de la ejercitación de algoritmos.
Cuaderno para PRIMARIA
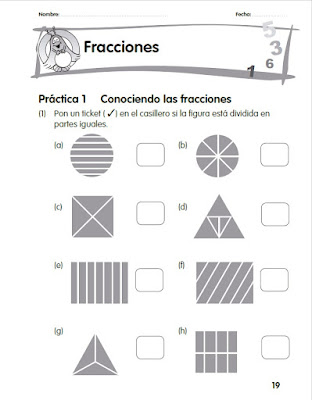
Ejercicios de FRACCIONES
Esto implica reconocer que hay distintos tipos de pensamiento lógico y matemático que se utilizan para tomar decisiones informadas, para proporcionar justificaciones razonables o refutar las aparentes y para ejercer la ciudadanía crítica, es decir, para participar en la preparación, discusión y toma de decisiones y para desarrollar acciones que colectivamente puedan transformar la sociedad.
Si vamos a desarrollar una competencia matemática específica en la básica y media, la pregunta “¿para qué me sirve eso?” tiene un gran valor, pues precisamente la competencia es para llegar al uso flexible y eficaz de ese conocimiento en la vida real.
CONTENIDO de material en PDF
👇Síguenos + materiales educativos👇
Tenemos que ser consecuentes: si queremos enseñar un tema de matemáticas para el desarrollo de la competencia respectiva, tenemos que tener clara la relación entre ese tema y el uso que tiene en la vida real del estudiante. Por lo tanto, tenemos que tener preparada una buena respuesta para el estudiante que se atreve a preguntarnos para qué sirve eso, y no despacharlo con cajas destempladas.
Deseas más materiales CLICK en el enlace👇
Por otro lado, los matemáticos también tienen razón en que no se pueden reducir las matemáticas de la educación básica secundaria al manejo de los fraccionarios en la vida cotidiana.
Cuaderno para ¡Nivel Primaria!
Full Ejercicios de FRACCIONES
Ejercicios de Fracciones. Afortunadamente, para el caso de los fraccionarios es fácil defender la selección de esta competencia, puesto que sirven para todo; además, otras competencias más importantes, como la modelación matemática de procesos de la vida real, necesitan por lo menos un buen nivel en el manejo de los números fraccionarios.
Nuestros niños y niñas están de acuerdo con Pitágoras, que también pensaba que el dos era el primer número. El cero no era número: ni siquiera lo conocían en ese tiempo. El uno tampoco era número: era el origen y principio de los números, pero no era número.
Pero una vez que uno arranca a contar: 1, 2, 3…, esos sí son los números de contar. Por eso, para mí, no para Pitágoras, el uno sí es un número: el primer número de contar.